Mit halbwegs aktueller Technik ist es viel einfacher als ich dachte, ein rudimentäres Kabelradar zu bauen. Eigentlich heißen die Dinger Zeitbereichsreflektometer, ein sperriger Begriff.
Also einfach den Avalanche-Impulsgenerator mit einem T an das Oszilloskop geklemmt und geguckt, was für ein Spannungsverlauf sich je nach angeschlossenen Elementen einstellt.
Vieles war wie erwartet: Beim Tektronix 2440 hält die 50-Ohm-Terminierung, was sie verspricht; mir fehlen Teiler, um ein Signal impedanzangepasst aufzuspalten.
Aber es gibt natürlich auch Überraschungen:
Mein Frequenzzähler, Modell HP 5334A, hat auch zuschaltbare eine 50-Ohm-Terminierung, die allerdings nur mäßig funktioniert. Dies liegt zum einen an der eingebauten Option 060 (rückseitige A-, B-, Trigger-Anschlüsse), die fehlangepasst angeschlossen ist. Und zum anderen daran, dass die 100 MHz Bandbreite der Eingänge auch einfachere Terminierungsmethoden erlauben. Daher treten wir keine toten Pferde, sondern uns angucken, welche Terminierung am besten funktioniert. Das ist, um es vorwegzunehmen, die interne Terminierung unter Einspeisung des Signals von hinten.
Ein andere Frequenzzähler, Modell Zopan PFL-28A-2, hat auch einen 200-MHz-Eingang mit 50-Ohm-Terminierung, macht aber keine bessere Figur als das HP-Modell. Da scheint ein Koppelkondensator am Anfang eingebaut zu sein, man misst jedenfalls keinen DC-Widerstand.
Unser abgeschaltetes TV-Kabel hat einen interessanteren Impedanzverlauf, siehe unten.
Einen Schwingkreis mit dem Impuls anzuregen, das wollte nicht so wie ich mir das dachte. Wahrscheinlich ist der Impuls zu nicht stark genug. Denn eigentlich ist er mit seinen weniger als 2 ns Breite (nicht vom Oszi täuschen lassen, hat ja nur 300 MHz Bandbreite, da treffen wir keine quantitativen Aussagen über das Gesehene!) für langsame Schwingkreise in grober Näherung ein Dirac-Impuls, sodass wir nach der Anregung die Impulsantwort erwarten. Ja, es passierte nur leider im Test nichts, eventuell waren meine Schwingkreise auch nur zu langsam mit ihrer Resonanz im kHz- oder einstelligen MHz-Bereich.
Galerie
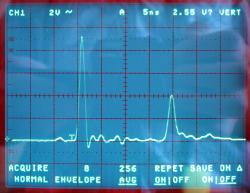
offenes Kabelende
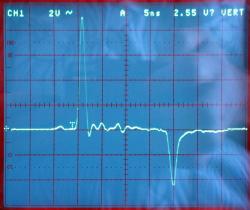
kurzgeschlossenes Kabelende
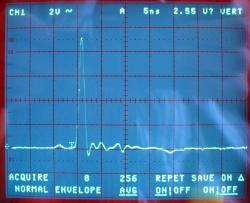
terminiertes Kabelende
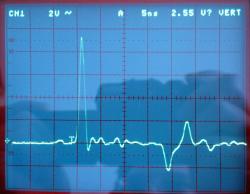
HP 5334A, Signal vorne, intern terminiert
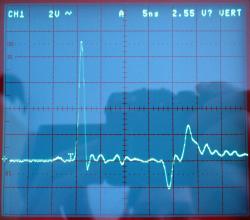
HP 5334A, Signal vorne, hochohmig
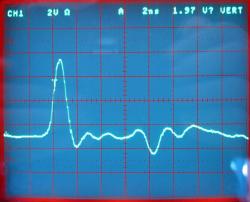
HP 5334A, Signal vorne, hinten terminiert
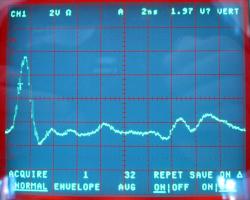
HP 5334A, Signal hinten, hochohmig
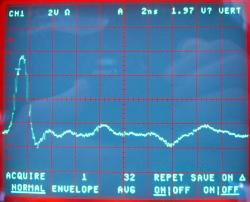
HP 5334A, Signal hinten, intern terminiert
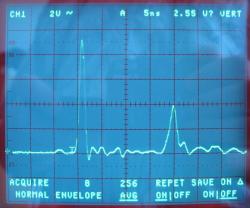
Zopan-Zähler, terminiert
Am TV-Kabel
Spannungsverlauf BNC-zu-F-Adapter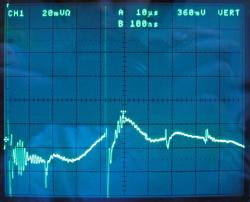

- 0 ns: Ursprungsimpuls, +6,8V Höhe
- 10 ns: Reflexion am Übergang zwischen BNC-Kabel (50 Ohm) und TV-Dose (75 Ohm), +1,5V Höhe, im Bild leider nicht sichtbar
- 173 ns: vielleicht ein Kabelknick? -70mV Höhe, die Impedanz ist also an dieser Stelle etwas geringer als 75 Ohm
- 427 ns: Reflexion am offenen Kabelende im Keller, +250mV Höhe
- 436 ns: -0,05V Höhe, 9 ns nach der Riesenreflexion. Eventuell ist das Kabelende mit einer Kappe verschraubt, die den Innenleiter nicht richtig kontaktiert, sodass der Großteil der einlaufenden Welle am offenen Ende reflektiert wird und nur ein geringer Teil an der mit der Kabelschirmung verbundenen Endkappe?
- 628 ns: kleine negative Delle, hier sehen wir die Kabelknick-Reflexion noch einmal
- 846 ns: Noch ein Zacken, der entspricht eindeutig wieder der TV-Dose. Wer es nicht glaubt, rechnet sich die Zeitdifferenzen aus, es stimmt.
Das sieht man alles gar nicht im Bild? Stimmt, ich habe die Zeitbasis zum Fotografieren vergrößert, so passt alles auf ein Foto. Durch Dehnung auf wenige ns/div erkennt man aber die beschriebenen Nadeln sehr gut, inklusive ihrer Höhe.
Ja und wie lang ist nun das Kabel in den Keller? Bei einem Verkürzungsfaktor von 0,84 (Pi mal Daumen, ungeschäumter Isolator, 75-Ohm-Koax) erhalten wir bei einer Verzögerung von 213,5 ns (Wir messen ja die Zeit, die der Impuls hin und zurück braucht!) eine Kabellänge von rund 54 Metern. Abzüglich der anderthalb Meter Messleitung von der TV-Dose bis zum Oszi sind das also 52 Meter Koaxkabel. Der Kabelknick wäre dann bei 21 m Länge ab meiner Dose. Ist etwas viel, oder? Ich wohne ja schließlich nicht mehr im Hochhaus.